20212_math_425a
Notes are available here. This is the file on which I have devoted most attention (and passion). Besides pure intellectual enjoyment, I did it hoping that it will help those who struggle with their first course in analysis. I hope you’ll like these notes and – if you are taking / about to take 425a – find them helpful.
- These notes were based on lecture recordings in spring 2021. More info can be found on Chapter 0 inside.
- Rest assured, this is as hard as 425a can get. Almost all sections of 425a, based on my experience, are significantly easier, covering about 70% of the content.
- Homeworks, if you also want something harder than usual. I did not take this course, so I did not write detailed solutions. Reach out to me if you need help on a specific one. 1 (infima & suprema) ‖ 2 (cardinalities) ‖ 3 (metric spaces) ‖ 4 (compact sets) ‖ 5 (limits) ‖ 6 (series) ‖ 7 (continuities) ‖ 8 (uniform continuities) ‖ 9 (differentiations) ‖ 10 (higher-order derivatives) ‖ 11 (integrations) ‖ 12 (more on integrations) ‖ 13 (uniform convergence) ‖ 14 (the guy who sent me the homeworks didn’t do HW14!)
- One frequent complaint I hear about 425a is its level abstraction, especially to those who have not experienced a proof-intensitve class before. To this end, in conjunction with Rudin’s rigorous content, I tried to add as many comments (mostly in italics) as possible to facilitate understanding via herustic method. These include:
- Visualization of abstract concepts, for example:
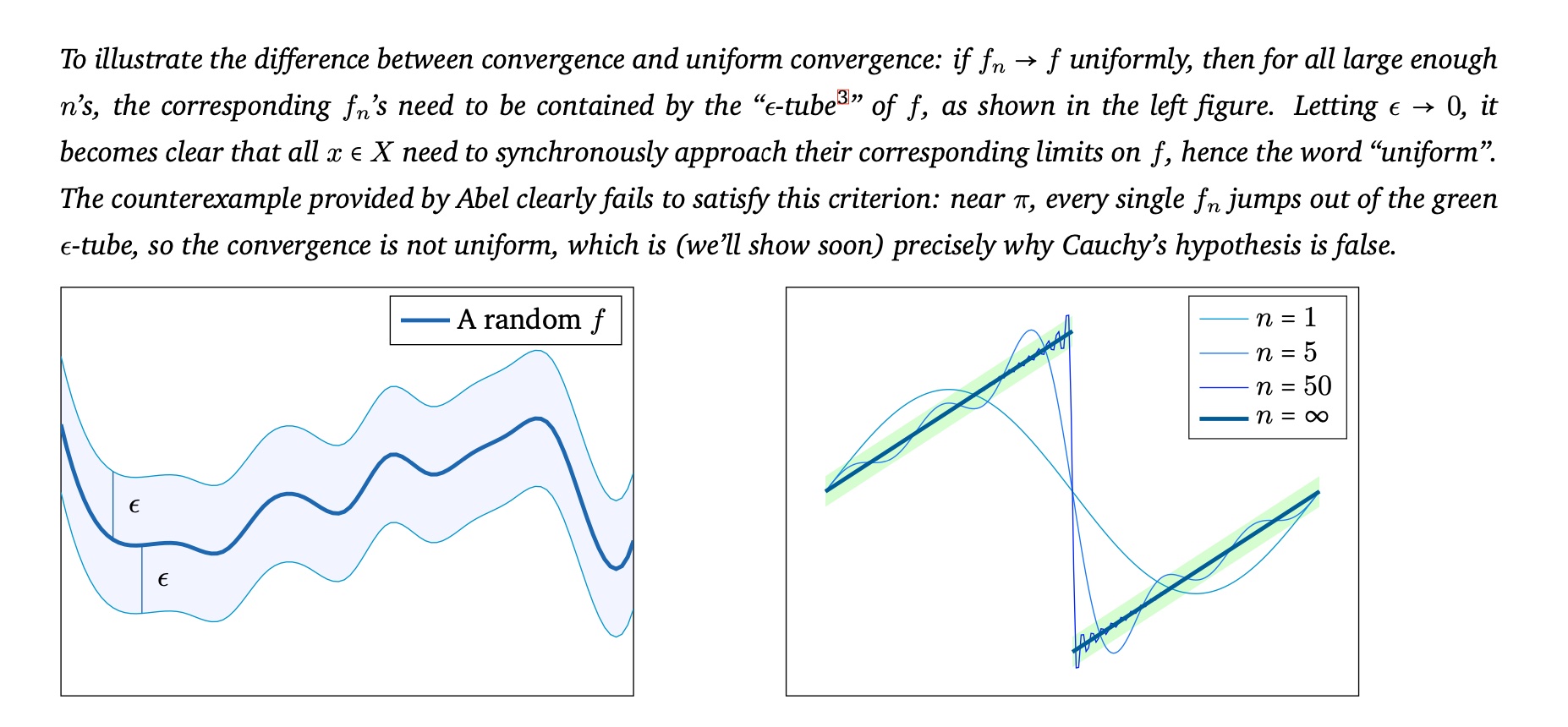
- Paragraphs on explaining the reason to learn particular theorems, for example Dini’s theorem (p.114-116).
- Paragraphs on explaining the underlying rationales behind a specific proof, for example the Bernstein polynomials used in the Weierstraß approximation theorem (p.135-136).
- Sentences commenting on specific techniques that are frequently used in analysis (e.g.
epsilon/3or1/n sequence). - Sentences commenting on the outline of a proof before starting it (e.g. Lebesgue’s number lemma on p.30). These mostly appear during the first half of the notes — as one gets increasing experienced with writing proofs, less guidance will be needed.
- Memes!

- Visualization of abstract concepts, for example: